Sorting Performance

Recently, I did some study on sorting algorithms and I’m amazed to find that the sort from standard Java Runtime Environment (JRE) is NOT as efficient as I expected. According to Java-DOC’s description:

public static <T> void sort(T[] a, Comparator<? super T> c)

Sorts the specified array of objects according to the order induced by the specified comparator. All elements in the array must be mutually comparable by the specified comparator (that is, c.compare(e1, e2) must not throw a ClassCastException for any elements e1 and e2 in the array).

This sort is guaranteed to be stable: equal elements will not be reordered as a result of the sort.
Implementation note: This implementation is a stable, adaptive, iterative mergesort that requires far fewer than n lg(n) comparisons when the input array is partially sorted, while offering the performance of a traditional mergesort when the input array is randomly ordered. If the input array is nearly sorted, the implementation requires approximately n comparisons. Temporary storage requirements vary from a small constant for nearly sorted input arrays to n/2 object references for randomly ordered input arrays.

The implementation takes equal advantage of ascending and descending order in its input array, and can take advantage of ascending and descending order in different parts of the the same input array. It is well-suited to merging two or more sorted arrays: simply concatenate the arrays and sort the resulting array.

The implementation was adapted from Tim Peters’s list sort for Python ( TimSort). It uses techniques from Peter McIlroy’s “Optimistic Sorting and Information Theoretic Complexity”, in Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, pp 467-474, January 1993.

I have checked another sort method’s description:

Implementation note: The sorting algorithm is a Dual-Pivot Quicksort by Vladimir Yaroslavskiy, Jon Bentley, and Joshua Bloch. This algorithm offers O(n log(n)) performance on many data sets that cause other quicksorts to degrade to quadratic performance, and is typically faster than traditional (one-pivot) Quicksort implementations.

So I’m curious to know how good the built-in sort is and whether my home-made sort can defeat it. It sounds like playing with AlphaGo, but I still decide to have a go. For the completeness, I include elementary sorting methods e.g. select sort, insert sort and shell sort, which have the performance of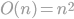
,
as well as more advanced sort e.g. merge sort and quick sort with the performance of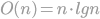
.
Here is the detailed source code.

Select sort

Comparable[] selectSort(Comparable[] t) {
  for (int i = 0; i < t.length; i++) {

    // find the smallest item from ith
    Comparable min = t[i];
    int jj = i;
    for (int j = i+1; j < t.length; j++) {
      if (isLess(t[j], min)) {
        min = t[j];
        jj = j;
      }
    }

    // exchange the ith with the smallest
    exchange(t, i, jj);
  }
  return t;
}

Insert sort

Comparable[] insertSort(Comparable[] t) {
  for (int i = 1; i < t.length; i++) {
    // insert the ith into the right place of 0..<i
    for (int j = i; j > 0; j--) {
      if (isLess(t[j], t[j-1])) {
        exchange(t, j, j-1);
      }
    }
  }
  return t;
}

Shell sort

Comparable[] shellSort(Comparable[] t) {
  int pace = 1, length = t.length;

  while (pace < length/3) pace = 3*pace + 1;

  while (pace > 0) {
    for (int j = 0; j < length; j += pace) {
      for (int k = j; k >= pace; k -= pace) {
        if (isLess(t[k], t[k-pace])) {
          exchange(t, k, k-pace);
        }
      }
    }
    pace = pace / 3;
  }
  return t;
}

Heap sort

Heap sort relies on Priority Queue, which itself is not a straightforward and therefore increase the overheads of resource consumption during sorting. It makes it the least competitive among all advanced sorting methods. For the brevity, I won’t post the full source code of Priority Queue:

public class PriorityQueue {

  public void add(Comparable item) {
    if (lastIndex == items.length-1) {
      throw new RuntimeException("Not support to enlarge queue capacity yet");
    }

    items[++lastIndex] = item;
    swim(lastIndex);
  }

  private void swim(int i) {
    int parentIndex = parent(i);
    if (parentIndex == 0) return;
    if (isBetter(items[i], items[parentIndex])) {
      exchange(items, i, parentIndex);
      swim(parentIndex);
    }
  }

  public Optional<Comparable> top() {
    if (isEmpty()) {
      return Optional.empty();
    }
    return Optional.of(items[1]);
  }

  public Optional<Comparable> pop() {
    Optional<Comparable> top = top();
    if (!top.isPresent()) {
      return top;
    }

    exchange(items, 1, lastIndex);
    items[lastIndex--] = null;
    // TODO shrink items' capacity

    sink(1);
    return top;
  }

  private void sink(int i) {
    int left = left(i), right = right(i);

    if (left > lastIndex) {
      return;
    }

    int exch = left;
    if (left < lastIndex && isBetter(items[left+1], items[left])) {
      exch = left + 1;
    }

    if (isBetter(items[exch], items[i])) {
      exchange(items, i, exch);
      sink(exch);
    }

  }

  private boolean isBetter(Comparable c1, Comparable c2) {
    return comparator.compare(c1, c2) > 0;
  }

  private int left(int index) {
    return index * 2;
  }

  private int right(int index) {
    return left(index) + 1;
  }

  private int parent(int index) {
    return index / 2;
  }

  public static Comparable[] heapSort(Comparable[] a) {
    PriorityQueue pq = new PriorityQueue(MIN, a.length);
    pq.addAll(a);

    Comparable[] result = new Comparable[a.length];
    int i = 0;
    while (!pq.isEmpty()) {
      result[i++] = pq.pop().get();
    }

    return result;
  }
}

Merge sort

Comparable[] mergeSort(Comparable[] t) {
  doMergeSort(t, 0, t.length-1, new Comparable[t.length]);
  return t;
}

void doMergeSort(Comparable[] t, int lo, int hi, Comparable[] buff) {
  if (lo >= hi) return;
  int mid = (lo + hi) / 2;
  doMergeSort(t, lo, mid, buff);
  doMergeSort(t, mid+1, hi, buff);
  merge(t, lo, mid, hi, buff);
}

void merge(Comparable[] t, int lo, int mi, int hi, Comparable[] buff) {
  if (lo >= hi) return;

  int index1 = lo, index2 = mi+1, len = hi - lo + 1;
  for (int i = 0; i < len; i++) {

    if (index1 > mi && index2 <= hi) {
      buff[lo + i] = t[index2++];
    } else if (index1 <= mi && index2 > hi) {
      buff[lo + i] = t[index1++];
    } else if (index1 <= mi && index2 <= hi) {
      if (isLess(t[index1], t[index2])) {
        buff[lo + i] = t[index1++];
      } else {
        buff[lo + i] = t[index2++];
      }
    } else { // not possible
      throw new RuntimeException();
    }
  }

  for (int i = 0; i < len; i++) {
    t[i+lo] = buff[lo + i];
  }
}

Quick sort

Comparable[] quickSort(Comparable[] t) {
  doQuickSort(t, 0, t.length-1);
  return t;
}

void doQuickSort(Comparable[] t, int lo, int hi) {
  if (lo >= hi) return;
  int anchor = makePartition(t, lo, hi, lo);
  doQuickSort(t, lo, anchor);
  doQuickSort(t, anchor+1, hi);
}

int makePartition(Comparable[] t, int lo, int hi, int sp) {
  exchange(t, lo, sp);
  Comparable anchor = t[lo];

  int j = lo+1, k = hi;
  while (j < k) {
    while (j <= hi && isLess(t[j], anchor)) j++;
    while (k >= lo && isLess(anchor, t[k])) k--;

    if (j < k) {
      exchange(t, j, k);
      j++;
      k--;
      continue;
    }
  }

  if (j > k) {
    exchange(t, lo, k);
    return k;
  } else {
    int anchorIndex = isLess(t[k], t[lo]) ? k : k-1;
    exchange(t, lo, anchorIndex);
    return anchorIndex;
  }
}

Performance & Conclusion

These are typical implementations without many well-known optimizations. The goal is to keep the code short and easy to understand. Let’s put them into use to see if they are competitive with JRE’s built-in sort.

Y-axis is millisecond, X-axis is the size of array to be sorted.

For each round, the performance is measured by generating 10 test data and sort these random data with different methods and take the mean time. The test data is shuffled in this way:

void shuffle(Comparable[] a) {
  for (int i = 0; i < a.length; i++) {
    exchange(a, i, random(0, i));
  }
}

From the chart we can see that all elementary sort methods start to struggle with the performance for arrays of 20K (an one-second waiting time is an obvious delay for user experience as well as a cross boundary transaction), while those advanced sort methods’ limits are around 2,000K.

Admittedly, modern compiler and CPU are competitive enough for even elementary sort methods to handle array within 10K. In terms of code complexity and footprint, both Select Sort and Insert Sort have a straightforward code structure and easy to read, so they can be good candidates for non-resource-critical use. Shell Sort, however, has a rather complicated code and has the most significant performance issue and therefore should not be used unless in the special circumstance that most adjacent elements have a far distance.

On the other hand, for large-scale applications, a decent sort method like Merge Sort or Quick Sort is the only choice when the sorting array consists of more than millions of data. Among these methods, Heap Sort has the least performance, Merge Sort falls behind when the data is over one million and Quick Sort manages to finish the sorting of one million within half a second.

Another interesting finding is although the benchmark of JRE’s built-in sort is stable for different inputs, it is beaten by my home-made Quick Sort when the size of incoming array is over one million. I did the same test several times and each time had the same conclusion.